¿Por qué pensar en los procedimientos a la hora de enseñar matemática?

Cuando enseñamos matemática, enseñamos conceptos, ideas. Por ejemplo, las operaciones aritméticas, y allí –caso emblemático–, la división. Hace tiempo que la experiencia nos muestra que no alcanza con “explicar” la división; con mostrárserla a los estudiantes y que la imiten lo mejor posible. Esa forma de enseñar no funciona (o, en todo caso, funciona para entrenar papagayos).

¿Y qué es lo que sí funciona? Sintéticamente, diremos que se construye sentido para un concepto en la medida en que se presenta como herramienta para resolver. Entonces, para dar sentido a la división, empezamos proponiendo problemas de división. E invitamos a los estudiantes a resolverlos.

Tomemos, como ejemplo, un clásico: Susana Horia tiene 84 zanahorias. Quiere armar bolsitas para repartir en su cumpleaños. En cada bolsita pondrá 7 zanahorias. ¿Cuántas bolsitas podrá armar?

Este problema se resuelve dividiendo. Pero también de varias otras formas: con distintos procedimientos. A continuación los presentaremos. 

Pero antes, alguien bien podría preguntarse: ¿para qué tanta vuelta si hay un procedimiento más corto y más cómodo (la división)? ¿Por qué no les mostramos eso que venimos a enseñar, y listo?

En principio, podríamos preguntarnos si la velocidad o la comodidad son valores en sí mismos, además de objetivos de enseñanza. Creemos que no.

Luego, vale preguntarse si la comodidad y la simpleza son absolutas. Es decir, quizás no valen igual para todos, ni tampoco funcionan del mismo modo en cualquier problema. Tal vez comodidad y simpleza dependan de las circunstancias, de quien resuelve y de la situación a ser resuelta.

Pero fundamentalmente, la pregunta pasa por la posición intelectual en que ubicamos a las y los estudiantes. Si se trata de enseñar un único y “eficiente” camino, entonces su lugar será el de la recepción, de la imitación, de meros seguidores a pasos dictados desde arriba. Es el puesto de la línea de montaje, de la alienación. Ser Dylan, ser Candela o ser un robot, así, es casi lo mismo.

Por el contrario, se puede ofrecer lugar para explorar y desplegar, con invitación a intercambiar. Así aparece lo que saben y, tensionándolo, se convoca a saber más. Se invita a continuar con lo conocido y no a romper con eso. Habilita una conexión, un diálogo entre lo viejo y lo nuevo. Es la única manera de que lo aprendido tenga sentido, en vez de ser reiteración enajenada. Cuando se convoca lo sabido, se destaca el lugar de conocedores. Cuando el problema se resuelve con caminos personales, de trabajo en comunidad, sobre los cuales el estudiante puede hacerse cargo, se destaca el lugar de producción.

En suma, alfabetizar matemáticamente nos ubica a todos como portadores y productores de cultura, no como simples y maquinales imitadores de ideas ajenas.

Entonces, esquemáticamente, los procedimientos posibles serían:

• Por representación gráfica y conteo
• Por restas sucesivas
• Por sumas sucesivas
• Por sumas agrupadas
• Por multiplicaciones
• Por división

Conteo
Una posibilidad es dibujar con paciencia las 84 zanahorias y encerrarlas en bolsitas de a 7. Luego contar las bolsitas y listo.

• 

  Desde luego que la representación de las zanahorias puede ser icónica (con dibujitos o con palitos).

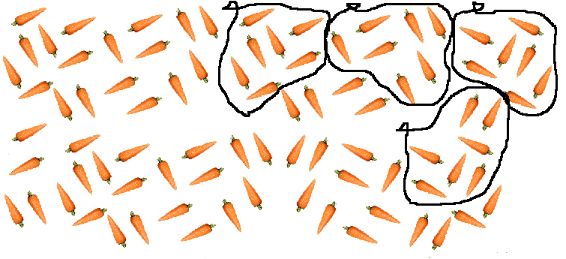
¿Vale este procedimiento? ¿Se acepta en clase?

Claro que vale. Y claro que se acepta, si la propuesta es hacerse cargo de la propia producción y no simplemente seguir las instrucciones de “quien manda”. Esta estrategia es lógica e indiscutible, si se contó y dibujó bien.

Peeero… Alguien podría decir que es tedioso (aunque sería una objeción subjetiva). Otro alguien podría señalar que es un procedimiento lento (sin embargo el aprendizaje no es una competencia contra el tiempo). Las objeciones sustanciosas no pasan por allí.

Los obstáculos aparecerían si en vez de 84 zanahorias fuesen, por ejemplo, 540. Y si en vez de bolsitas de 7 tuviésemos bolsones de 70 zanahorias. Ahí sí: contar sería imposible.

Por eso justamente trabajamos con las variables didácticas: con ciertas modificaciones, los docentes habilitamos y entorpecemos estrategias invitando a avanzar, tanto más por necesidad de quien resuelve que por súplicas de quien enseña.

Restas sucesivas

Tenemos las 84 zanahorias. Armamos una bolsa con 7. Entonces nos quedan 84 – 7 = 77 zanahorias sueltas.

Armamos otra bolsa. Ahora nos quedan 77 – 7 = 70 zanahorias sueltas.

Seguimos armando bolsas. Otra más. Nos quedan 70 – 7 = 63 zanahorias.

Y así seguimos embolsando hasta que no quedan más zanahorias disponibles.

      84 – 7 = 77
      77 – 7 = 70
      70 – 7 = 63
      63 – 7 = 56
      56 – 7 = 49
      49 – 7 = 42
      42 – 7 = 35
      35 – 7 = 28
      28 – 7 = 21
      21 – 7 = 14
      14 – 7 = 7
        7 – 7 = 0

Muy bien. Todo embolsado. ¿Y cuántas bolsas hemos armado? ¿Dónde lo dice?

Lo dice en la cantidad de veces que sacamos 7. Si contamos, son 12 veces que restamos. Por lo tanto, pudimos armar 12 bolsas.

¿Vale esta estrategia? Claro que vale. ¿Por qué no?

Restar es incómodo, pero no imposible. Se pueden usar los dedos incluso. Pero vale.

Nuevamente, como en el caso del conteo, se complicaría si el tamaño de los números fuera otro.

Pero esta estrategia se adapta con más versatilidad. La modificación de la variable didáctica debería ser más sutil. Porque si fueran 840 zanahorias y 70 en cada bolsa, las cantidad de restas a hacer sería la misma. No se dificultaría el procedimiento, por más que aumenten los tamaños.

En cambio, si fueran 840 zanahorias y solo 7 por bolsa, ahí sí: restar sería insufrible.

 

Sumas sucesivas

Tomamos 7 zanahorias y armamos una bolsa. Tomamos otras 7 para hacer otra. Ya llevamos 7 + 7 = 14 zanahorias embolsadas.

Juntamos otras 7 zanahorias más. Y ya embolsamos 14 + 7 = 21 zanahorias.

Y así seguimos coleccionando de a 7 hasta llegar al total de 84.

¿Cuántas bolsas hemos armado en este proceso?

La cantidad de veces que sumamos 7.

Si detalláramos la cuenta, veríamos que son 12, evidentemente.

El procedimiento es análogo al de las restas sucesivas. La única diferencia es que sumar suele ser más fácil que restar. Es más cómodo.

Sumas agrupadas
Tenemos que juntar de a 7 hasta llegar a 84. Podríamos ir juntando de a una bolsa, como en la estrategia anterior. Pero también podríamos ir armando de a varias bolsas.
         1 bolsa     →      7 zanahorias
        2 bolsas     →    14 zanahorias    (7 + 7)
        4 bolsas     →    28 zanahorias    (14 + 14)
        8 bolsas     →    56 zanahorias    (28 + 28)
      12 bolsas     →    84 zanahorias    (56 + 28)
Es una manera de llegar “más rápido”, con menos pasos, hasta el total.

Otra forma “inteligente”, más pícara, de agrupar es usando los múltiplos de 10, porque son resultados fáciles de obtener (disponibles en el repertorio de cálculo).
        1 bolsa     →    7 zanahorias
     10 bolsas     →    70 zanahorias
    100 bolsas     →    700 zanahorias (nos recontrapasamos)
      20 bolsas     →    140 zanahorias (también no pasamos)
      11 bolsas     →    77 zanahorias (70 + 7)
      12 bolsas     →    84 zanahorias (77 + 7)

Multiplicaciones

Si manejamos la multiplicación y tenemos, por ejemplo, una calculadora, podemos ir tanteando.

Sabemos que varias veces 7 debe dar 84. Esa cantidad de veces 7 será la cantidad de bolsas.

Por ejemplo, 7×3 sería la cantidad de zanahorias en 3 bolsas. Es 21. Por lo tanto, necesitamos más de 3 bolsas.

Probamos con 7×10 = 70. Todavía falta para llegar a 84.

Probamos con 7×15 = 105. Nos pasamos de 84. Entonces deben ser menos bolsas.

Probamos con 7×13 = 91. Nos pasamos, pero por poquito…

Probamos con 7×12 = 84. ¡Llegamos al total! Encontramos la respuesta. Son 12 bolsas.

¿Vale así? ¿O es una forma de trampa?
Sí vale. Y no es trampa.

Pero sin la calculadora también podríamos usar multiplicaciones. Buscamos en la Tabla Pitagórica, en la columna del 7, qué valor nos da 84. Pero vemos que no está. ¿Entonces?
Entonces usamos el que más se aproxima: 7×10 =70.

Vemos ahora cuánto nos falta para lo que necesitábamos: 84 – 70 = 14.

Ahora buscamos en la Tabla Pitagórica, columna del 7, qué valor da 14. Y lo hallamos: 7×2 = 14.

Entonces sabemos que:

/ 7×10    = 70 \
\ 7× 2     = 14 /
                         
→ 7×12  = 84 ¿

Por lo tanto son 12 las bolsas que necesitaba.
Pero… ¿cómo? ¿Por qué tanta multiplicación? ¿No era que queríamos enseñar la división? 

Justamente, como queríamos enseñar la división, habilitamos estos caminos. Veremos que la división es básicamente hacer lo que acabamos de hacer. Solo que se suele presentar en una disposición espacial más elegante. Pero dividir es sustancialmente eso.

División

Finalmente, si identificamos que el problema responde a un reparto equitativo, podríamos usar la división como herramienta para resolver.

Dividiendo el total (84) entre el tamaño de la parte (las 7 zanahorias de la bolsa), obtendremos la cantidad de partes (84 : 7 = 12 bolsas).

Y en el caso de saber que la división funciona ¿cómo haríamos esa división?

Podría ser con la calculadora, si la tenemos a mano. ¿Por qué no?

Y si no, podríamos dibujar la “casita” y poner los números como nos enseñaron hace tiempo:
                        84   |  7   

¿Y ahora que tenemos los números en la hoja? ¿Qué hacemos?

Casi lo mismo que hacíamos en el procedimiento anterior, pero más ordenadito. La división es un tanteo de multiplicaciones, más metódico nomás. Continuidad y superación, no ruptura.

Por eso es tan importante tener en cuenta los distintos procedimientos: convocarlos, estimularlos sin imponer. Porque sobre ellos se construirá el sentido para esta operación tan compleja. Si no, caeremos una vez más en la técnica impuesta para copiar.

¿Y cuál sería el problema de ese modo de enseñanza tan extendido a lo largo de la historia (y con el cual, seguramente, muchos de nosotros hemos sido “adiestrados”)?

No es ninguna tragedia, desde luego, pero vale preguntarse qué se aprende aprendiendo a repetir, qué clase de sujeto se está formando, para qué concepción de ciudadanía, para qué modelo de sociedad, qué sueños pedagógicos e ideológicos, en definitiva, nos mueven en la diaria tarea.

*Horacio Cárdenas es maestro de escuela primaria y profesor en formación docente en el área de matemática.